Maxima and Minima of Quadratics and Reciprocals of Quadratics
To find the minimum or maximum of a quadratic we complete the square expressing the function in the form
If
the minimum will be where
so
and the minimum is at
If
the maximum will be wheresoand the maximum is at
For example, to find the minimum of
complete the square to get
then the minimum is at
To find the maximum of
complete the square to get
then the maximum is at
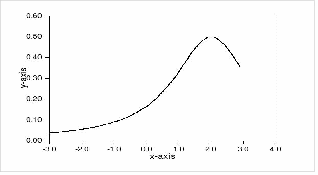
We might also have to find the maxima of reciprocal quadratics such as
The quadratic here can have no roots if it is to have a maximum, or else at those roots we would have
which has no value, and close to those roots the graph would tend to
As before we complete the square to get
To maximise y we have to minimise the denominator ie minimise
This has a minimum at
hence
has a maximum at
This is illustrated below. If the numerator were negative we would follow the same procedure, completing the square but now find a minimum, in this case at
