Two events A and B are mutually exclusive if they cannot both occur, either at the same time, or one after the other, depending on the circumstances. If they are mutually exclusive and![]()
![]() and
and![]() are the probabilities of events A, B or both A and B occurring respectively, then A and B are mutually exclusive if
are the probabilities of events A, B or both A and B occurring respectively, then A and B are mutually exclusive if![]()
The definition extends naturally to sets. Two sets A and B are mutually exclusive if![]() or
or ![]() There is no intersection.
There is no intersection.
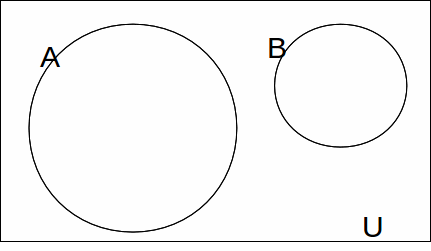
Events A and B are mutually exhaustive if either A must occur or B must occur or both. This then means that![]() If events A and B are mutually exhaustive then
If events A and B are mutually exhaustive then![]() This definition also extends naturally to sets. If sets A and B are mutually exhaustive then
This definition also extends naturally to sets. If sets A and B are mutually exhaustive then![]() or
or![]() If A and B are also mutually exclusinve then
If A and B are also mutually exclusinve then![]()
Events A and B are independent if event A does not affect the probability of event B and vice versa.![]()
![]() and
and![]() satisfy the equation
satisfy the equation![]() Alternatively, we can consider that event B has happened, and then consider the probability that A will happen. This is called 'conditional probability' – the probability of A happening conditional on B having happened, and is written
Alternatively, we can consider that event B has happened, and then consider the probability that A will happen. This is called 'conditional probability' – the probability of A happening conditional on B having happened, and is written![]() The equation for conditional probability is
The equation for conditional probability is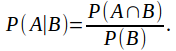
If A and B are independent then![]() so
so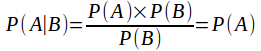 which states the obvious fact that A is independent of B.
which states the obvious fact that A is independent of B.
