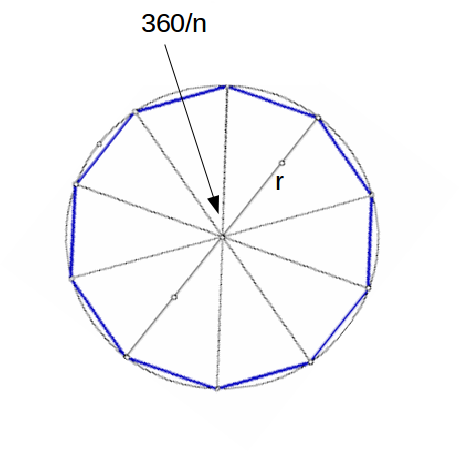
\[n\]
sides is inscribed in a circle of radius \[r\]
, with the vertices of the polygon touching the circle.From the centre of the circle lines are drawn to each vertex, and
\[n\]
triangles are formed. The angle of each triangle at the centre of the circle is \[\frac{360}{n} \equiv \frac{2 \pi}{n}\]
, and the length of the side opposite this angle is is\[\begin{equation} \begin{aligned} a &= \sqrt{r^2+r^2-2 \times r \times r \times cos( \frac{2 \pi}{n}} \\ &= r \sqrt{2-2 cos( \frac{2 \pi}{n}} \\ &= r \sqrt{2} \sqrt{1-cos( \frac{2 \pi}{n}} \\ &= r \sqrt{2} \sqrt{2 sin^2 \frac{\pi}{n}} \\ &= 2 r sin \frac{\pi}{n} \end{aligned} \end{equation}\]
.
\[n\]
such triangles, so the perimeter of the polygon is \[n \times 2 r sin \frac{\pi}{n} \]
.As the number of sides gets larger
\[sin (\frac{\pi}{n}) \]
tends to \[\frac{\pi}{n}\]
, so the perimeter of the polygon tends to \[n \times 2r \frac{\pi}{n}=2 \pi r\]
. 