Theorem
The linear congruence![]()
-
Has solution if and only if
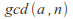 divides
divides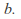
-
Has a unique solution if
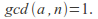
-
Has
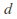 solutions, where
solutions, where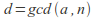 and
and 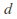 divides
divides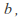 given by the unique solution
given by the unique solution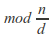 of the congruence
of the congruence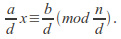
Proof: The linear Diophantine equation![]() has solutions if and only if
has solutions if and only if![]() divides
divides![]() from which 1. follows.
from which 1. follows.
For 2. suppose![]() If
If![]() is one solution of
is one solution of![]() the general solution is
the general solution is![]() but
but![]() so
so![]() is the only solution of
is the only solution of![]()
For 3. if![]() and
and![]() divides
divides![]() then
then![]() but
but![]() so the last congruence has a unique solution
so the last congruence has a unique solution![]() Hence the integers satisfying
Hence the integers satisfying![]() are
are![]() None of these are congruent (mod n) because none differ by n and for any integer
None of these are congruent (mod n) because none differ by n and for any integer![]() is congruent
is congruent![]() to one of them since if
to one of them since if![]() as given by the Division Algorithm, then
as given by the Division Algorithm, then![]() so these are the solutions to
so these are the solutions to![]()
Example: Solve![]()
![]() so the congruence has three solutions (mod 21)
so the congruence has three solutions (mod 21)
Cancel 3 to give![]() Multiply the congruence by a number so that the coefficient of
Multiply the congruence by a number so that the coefficient of![]() is 1. We multiply by 2 to give
is 1. We multiply by 2 to give![]() and reduce both sides (mod 7) to give
and reduce both sides (mod 7) to give![]() Then
Then![]() and
and![]() are the other solutions.
are the other solutions.
Example: Solve![]()
![]() so the congruence is unchanged.
so the congruence is unchanged.
Multiply by three to give![]() and reduce (mod 26) to give
and reduce (mod 26) to give![]() This is the only solution.
This is the only solution.
