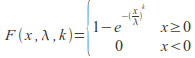The probability density function of a Weibull random variable X is
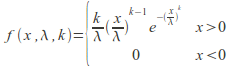
where![]() is the shape parameter and
is the shape parameter and![]() is the scale parameter. This is shown below.
is the scale parameter. This is shown below.
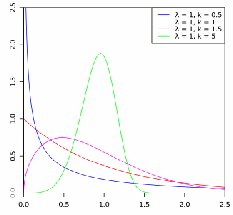
If![]() is a "time-to-failure", the distribution gives a distribution for which the failure rate is proportional to a power of time. The failure rate here is
is a "time-to-failure", the distribution gives a distribution for which the failure rate is proportional to a power of time. The failure rate here is![]() The shape parameter,
The shape parameter,![]() is that power plus one, and this parameter can be interpreted directly as follows:
is that power plus one, and this parameter can be interpreted directly as follows:
-
k<1 indicates that the failure rate decreases over time. This indicates a high initial failure rate. As these initial failures are overcome, only the 'healthy' long lived ones remain.
-
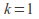 indicates that the failure rate is constant, suggesting failure is due to random events.
indicates that the failure rate is constant, suggesting failure is due to random events. -
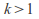 Indicates the failure rate increases over time, indicating an aging process as with many manufactured goods.
Indicates the failure rate increases over time, indicating an aging process as with many manufactured goods.
The cumulative distribution function is![]()
The mean and variance of the Weibull distribution are![]() and
and![]() respectively.
respectively.
The moment generating function can best be expressed as the integral![]()
This integral is not elementary.