Suppose that
and
are functions continuously differentiable on a region
As
ranges over
the point
generates a region
in the
plane.
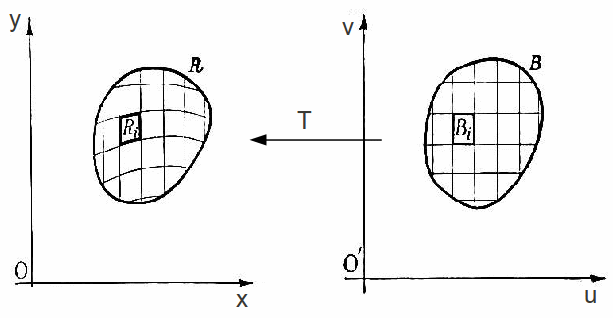
If the mapping
is one to one on the interior of
and the Jacobian
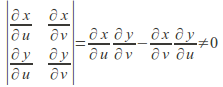on the interior of B then the area of
Suppose then that we want to integrate some continuous function
over
If the integral is intractable then we can change variables to
and integrate overinstead, because
Proof: Break upinto
smaller regions
We can write
The last expression is a Riemann sum for
and the expression tends to this integral as the diameter of the
tends to zero.