The Mean Value Theorem

Ifis a differentiable function with a continuous derivative and ifare any two points then there is a point betweenandat which

This result is also `geometrically obvious' once you draw the picture.

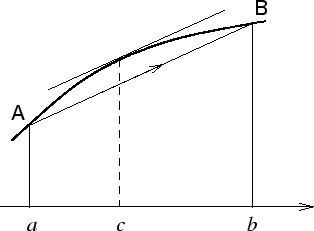
Mean Value Theorem: somewhere between a and b , the graph must be parallel to the chord

The expressionis just the slope of the chordSo the theorem is saying that there must be a pointbetweenandat which the slope of the graph is equal to the slope of the chord

This may seem very simple--it is very simple--but it is also very important. In most of its applications we think of the result in the following way, which is easily derived.

(Note that the theorem does not tell us what c is--just that it must be there.)

Here's a simple application of this theorem. Suppose thatbetweenand Thenmust be positive (whatever c is). Somust be bigger thanSo, in an obvious sense, the function must be increasing.

Here's another typical application. LetThenSo we must have This result is rubbish. For example, tan() = tan(0) = 0. But 0 - 0 is not bigger than - 0. What's gone wrong?

The problem here is thatis not a differentiable function between 0 and--it blows up atWhen using these theorems, no matter how `obvious' they are, you really must check that the conditions of the theorem are precisely satisfied.