We can integrate to find an area using the expression
where
is the region whose area is to be found.
Compare this with Green's theorem:
If we find
and
such that
then the right hand side will be the expression for the area of
For example, use Green's theorem to find the area of the ellipse with cartesian equation
An ellipse is a simple (no holes) closed curve.
Choose
and
so thatthe the right hand side becomes 1 and we have
We now transform to polar coordinates
and
By taking
as increasing from 0 to
we are orienting the curve counterclockwise, hence in a positive direction.
and
then
In practiceandare chosen so that the final integration becomes tractable.
Example: Find the area of the triangle below.
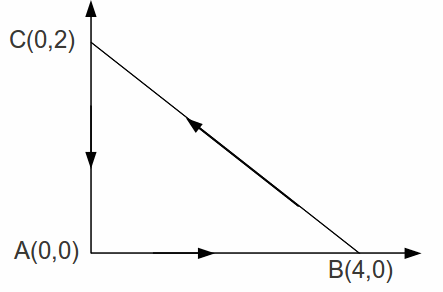
Take
thenand
On
and on
so only the middle integral contributes to the area.
On BS,
so