\[A = \int_S dS\]
where \[S\]
is the surface of the sphere.We can parametrize the surface in terms of angles
\[\phi, \theta\]
.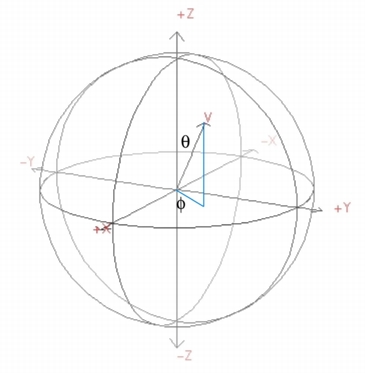
\[0 \leq \theta \leq \pi , 0 \leq \phi \leq 2 \pi\]
With this parametrixation we can write the integral as \[A =\int_{\theta} \int_{\phi} | \frac{\partial \mathbf{r}}{\partial \theta} \times \frac{\partial \mathbf{r}}{\partial \phi} | d \theta d \phi \]
\[\mathbf{r} = r sin \theta cos \phi \mathbf{i} + r sin \theta sin \phi + r cos \theta \]
Hence
\[\frac{\partial \mathbf{r}}{\partial \theta} =r cos \theta cos \phi \mathbf{i} + r cos \theta sin \phi - r sin \theta \]
\[\frac{\partial \mathbf{r}}{\partial \phi} =-r sin \theta sin \phi \mathbf{i} + r cos \theta cos \phi \]
\[||\frac{\partial \mathbf{r}}{\partial \theta} \times \frac{\partial \mathbf{r}}{\partial \phi}| = \left| \begin{array}{ccc} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ r cos \theta cos \phi & r cos \theta sin \phi & -r sin \theta \\ -r sin \theta sin \phi & r cos \theta cos \phi & 0 \end{array} \right| = =r^2 sin \theta \]
The integral becomes
\[\begin{equation} \begin{aligned} A &= \int^{\pi}_0 \int{2 \pi}_0 r^2 sin \theta d \phi d \theta \\ &= 2 \pi r^2 \int^{\pi}_0 sin \theta d \theta \\ &= 2 \pi r^2 [-cos \theta]^{\pi}_0 \\ &= 2 \pi r^2 (- cos \pi -(-cos 0)) \\ &= 4 \pi r^2 \end{aligned} \end{equation}\]
