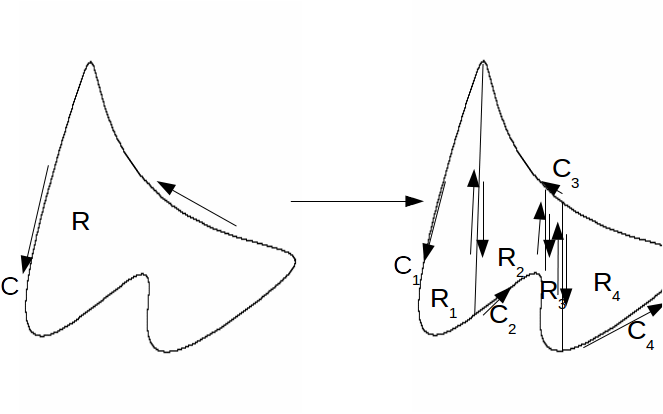
\[R_1 , R_2 , ..., R_n\]
, \[ \oint_{C_i} P \: dx + Q \: dy = \int \int_{R_i} \frac{ \partial Q}{\partial x} - \frac{ \partial P}{\partial y} dx \: dy \]
We can write Down a corresponding equation for each of
\[i=1,2,...,n\]
Adding them all gives
\[\begin{equation} \begin{aligned} \oint_{C_1} P \: dx + Q \: dy + \oint_{C_2} P \: dx + Q \: dy +...+ \oint_{C_n} P \: dx + Q \: dy &= \int \int_{R_1} \frac{ \partial Q}{\partial x} - \frac{ \partial P}{\partial y} dx \: dy + \int \int_{R_2} \frac{ \partial Q}{\partial x} - \frac{ \partial P}{\partial y} dx \: dy +... \\ &+ \int \int_{R_n} \frac{ \partial Q}{\partial x} - \frac{ \partial P}{\partial y} dx \: dy \end{aligned} \end{equation} \]
Which simplifies by the properties of integration to
\[\oint_{C} P \: dx + Q \: dy = \int \int_{R} \frac{ \partial Q}{\partial x} - \frac{ \partial P}{\partial y} dx \: dy \]
