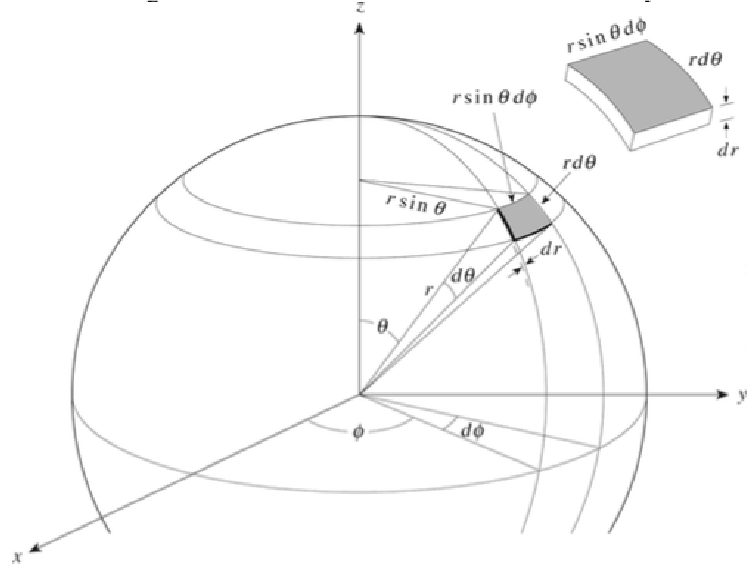
\[dr, \; r d \theta , \; r sin \theta d \phi\]
at right angles, so the volume of the cuboid \[dV \simeq r^2 sin \theta dr d \theta d \phi \]
.The approximation becomes better as
\[dr, \; d \phi \; d \theta \rightarrow 0\]
.We can also approximate an element of surface area as the area of a rectangle of base and height
\[r sin \theta d \phi , \; r d \theta , \]
respectively so \[dA \simeq r d \phi d \theta\]
.Again the approximation improves as
\[ d \phi \; dz \rightarrow 0\]
. 