Convergents of Continued Fractions

We start with a definition. For a finite continued fractionthe kth convergentis the finite continued fraction

Example: The simple finite continued fractionhas convergents

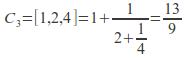
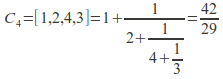
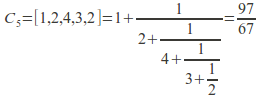
We can evaluate the convergents recursively, using The Second Continued Fraction Identity:

Example: Find the convergents of the simple finite continued fraction

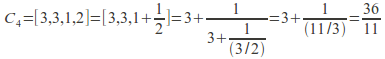
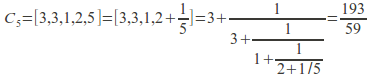
This definition of convergents carries over in a natural way to infinite continued fractions.