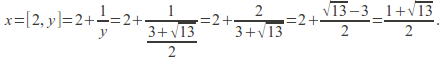An infinite continued is fraction is of the form
The continued fraction always converges. In fact the numerators p-k of the kth convergents forms a decreasing sequence and the denominators form an increasing sequence, so the quotient p-k over q-k converges to a limit. Given a periodic infinite continued fraction, we can find the value of the fraction as in the following example.
In this continued fraction the sequence 313 generates the fraction so we can write
Hence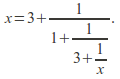
We can rearrange this into a quadratic equation.
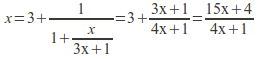
Clearing the fractions now gives
which simplifies to
which has solutions
is positive so we ignore the negative square root which gives a negative value for
to obtain
Example: Find the value of
Let
then
This has solutions
taking the positive square root. Then