Let![]() be an odd prime and
be an odd prime and![]() The Legendre symbol
The Legendre symbol![]() is defined as
is defined as
![]()
For example,![]() and
and ![]()
The Legendre symbol has the following properties for![]() where
where![]() is an odd prime.
is an odd prime.
-
If
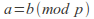 then
then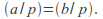
-
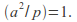
-
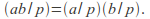
-
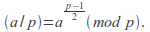
-
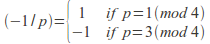
The Legendre symbol can be used to decide if some equations![]() have solutions. If the equation is quadratic for example,
have solutions. If the equation is quadratic for example,![]() then the existence of solutions reduces to whether
then the existence of solutions reduces to whether![]() is a quadratic residue of
is a quadratic residue of![]()
For the equation![]() the discriminant is
the discriminant is![]()
![]()
![]()
![]()
![]() since
since![]() by 5 above.
by 5 above.
![]()
![]()
![]()
The Legendre symbol my be used to find all the quadratic residues (mod p). If![]() then of course1, 4, 9, 16, 25, 36 are quadratic residues.
then of course1, 4, 9, 16, 25, 36 are quadratic residues.
![]() so -1 is a quadratic residue from 5 above.
so -1 is a quadratic residue from 5 above.
![]() so 33 is a quadratic residue.
so 33 is a quadratic residue.
Similarly,![]() and
and![]() are quadratic residues.
are quadratic residues.
Also![]() and
and![]() so 3 and 7 are quadratic residues. Using these and
so 3 and 7 are quadratic residues. Using these and![]() then give
then give
![]() and
and![]() so 34 and 30 are quadratic residues.
so 34 and 30 are quadratic residues.
![]() and
and![]() so 11 and 27 are quadratic residues and so are
so 11 and 27 are quadratic residues and so are![]() and
and![]()
