The Goldbach conjecture is one of the most famous unsolved problems in number theory. It states that every number from 4 onwards can be written as a sum of two primes in at least one way.
This is illustrated for the first ten even numbers from 6 upwards:
4=2+2
6=3+3
8=3+5
10=3+7=5+5
12=5+7
14=3+11=7+7
16=3+13=5+11
18=5+13=7+11
20=3+17=7+13
22=3+19=5+17=11+11
24=5+19=7+17=11+13
The number of ways that a number can be so expressed seems to increase as the number gets bigger. This is illustrated below
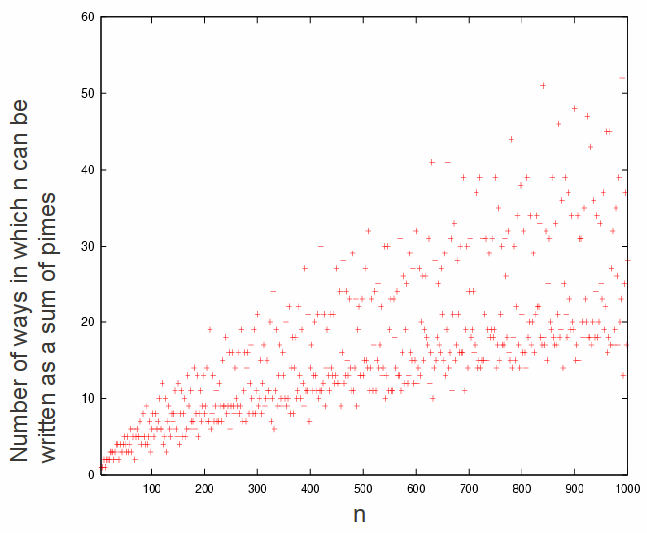
Computers have verified Goldbach's conjecture for even numbers up to 10^8 and steps are being made towards a proof. In 1937 it was proved that every sufficiently large number is the sum of three primes, at most which implies that every sufficiently large even number is the sum of four primes at most.
