The number of colours , called the chromatic number, sufficient for map colouring on a surface of genus
is given by the Heawood conjecture,
where
is the floor function. Necessity is also true with two exceptions: the sphere (which requires the same number of colours as the plane) and the Klein bottle.
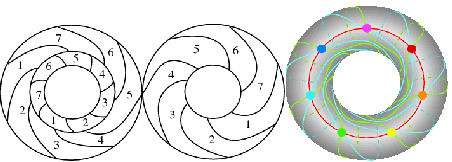
An n -holed torus therefore requires
colours. For
the first few values ofare 4, 7, 8, 9, 10, 11, 12, 12, 13, 13, 14, 15, 15, 16. A set of regions requiring the maximum of seven regions is shown above for a normal torus
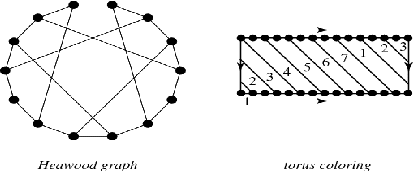
The above figure shows the relationship between the Heawood graph and the 7-color torus colouring.