Suppose we observe a random variable
and wish to make inferences about another random variable
whereis drawn from some distribution
From the definition of conditional probability,
Again from the definition of conditional probability, we can express the joint probability by conditioning onto give
Substituting (2) into (1) gives Bayes’ theorem:
If there are
mutually exclusive possible outcomes for
then we can write
hence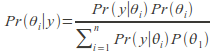
Bayes theorem gives rise to some surprises. Many people diagnosed with disease are falsely diagnosed. Suppose that one in a thousand adults has a disease. When an individual has a disease, a positive result will be returned 99% of the time, while a positive result will be returned for 2 % of individuals who do not have the disease. Let
and
then
and
so
and
Less that one in twenty positive diagnoses are actually true positives. More than 95% of positives results are false positives.