Given two jointly distributed random variables![]() and
and![]() the conditional probability distribution of
the conditional probability distribution of![]() given
given![]() is the probability distribution of
is the probability distribution of![]() when
when![]() is known to be a particular value.
is known to be a particular value.
|
|
|||||
|
0 |
1 |
2 |
|
||
|
|
0 |
0.05 |
0.05 |
0 |
0.1 |
|
1 |
0.2 |
0.05 |
0.15 |
0.4 |
|
|
2 |
0.1 |
0.06 |
0.04 |
0.2 |
|
|
3 |
0.1 |
0.08 |
0.12 |
0.3 |
|
|
|
0.45 |
0.24 |
0.31 |
||
1The conditional probabilities for![]() given
given![]() are obtained by dividing each entry by the righthandmost entry shown in bold, giving
are obtained by dividing each entry by the righthandmost entry shown in bold, giving
|
|
|||||
|
0 |
1 |
2 |
|
||
|
|
0 |
|
|
|
0.1 |
|
1 |
|
|
|
0.4 |
|
|
2 |
|
|
|
0.2 |
|
|
3 |
|
|
|
0.3 |
|
|
|
0.45 |
0.24 |
0.31 |
||
1Note that each row sums to one.
The conditional probabilities for![]() given
given![]() are obtained by dividing each entry by the bottom entry in the column shown in bold, giving
are obtained by dividing each entry by the bottom entry in the column shown in bold, giving
|
|
|||||
|
0 |
1 |
2 |
|
||
|
|
0 |
|
|
|
0.1 |
|
1 |
|
|
|
0.4 |
|
|
2 |
|
|
|
0.2 |
|
|
3 |
|
|
|
0.3 |
|
|
|
0.45 |
0.24 |
0.31 |
1 |
|
Note that each column sums to one.
To generalise, for discrete random variables, the conditional probability mass function of![]() given (the occurrence of) the value
given (the occurrence of) the value![]() of
of![]() with
with![]() can be written, using the definition of conditional probability, as:
can be written, using the definition of conditional probability, as:
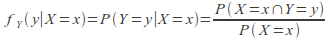
We can write down also the probability distribution of
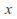 given
given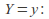
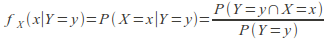
From these we deduce
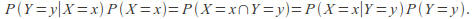 (1)
(1)Similarly for continuous random variables, the conditional probability density function X given the value y of Y is
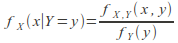 and the conditional probability density function of
and the conditional probability density function of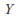 given the value
given the value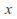 of
of 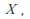 can be written as
can be written as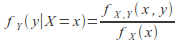
where
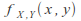 gives the joint density of
gives the joint density of and
and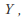 while
while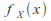 for
for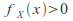 gives the marginal distribution function for
gives the marginal distribution function for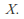
Similarly as for (1) we can write
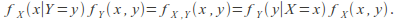
If for discrete random variables
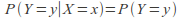 for all
for all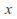 and
and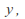 or for continuous random variables
or for continuous random variables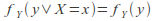 or
or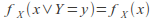 or equivalently
or equivalently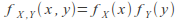 for all
for all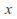 and
and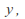 then
then and
and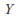 are independent.
are independent.As a function of
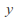 given
given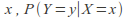 is a probability and so the sum over all
is a probability and so the sum over all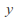 (or integral if it is a conditional probability density) is 1. Seen as a function of
(or integral if it is a conditional probability density) is 1. Seen as a function of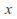 for given
for given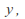 it is a likelihood function, so that the sum over all
it is a likelihood function, so that the sum over all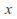 need not be 1.
need not be 1.
