The hypergeometric distribution is closely related to the binomial distribution. The binomial distribution is the model for sampling with replacement from a finite collection, or sampling with or without replacement from an infinite collection, with success or failure the possible outcomes, or the approximate distribution without replacement if the collection is large but finite. The hypergeometric is the exact distribution for the number of successes (or failures) in any sample drawn from a finite collection, without replacement.
The assumptions leading to the hypergeometric distribution are:
-
The population from which the samples are drawn is finite.
-
Each individual selection drawn from the sample can be classified as a success or failure and there are
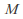successful individuals in the population. -
A sample of
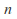individuals is drawn in such a way that each subset of size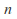is equally likely to be chosen.
If the population has M successful individuals in a population of size
then the number of successes
in a sample of sizedrawn from the population,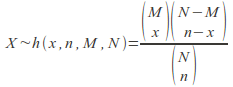
for satisfying
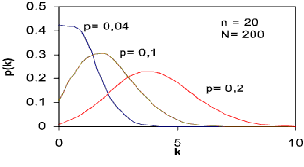
The mean and variance are given by
for
and some values of
are shown below.
Example: Five individuals from a near extinct species consisting of only 25 animals are caught, tagged and re - released. Some time later a sample of 10 animals is selected. What is the probability that 2 of this sample are wearing tags?
The distribution is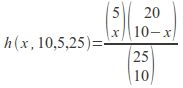
hence
is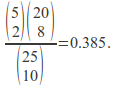
Suppose instead the population sizeis not known. We wish to estimate
We can estimate
as
hence
If
then 