The Negative Binomial Distribution

The negative binomial distribution has the following requirements:

1. A sequence of independent trials.

2. Each trial can result in success (S) or failure (F).

3. The probability of success,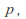is a constant.

4. Trials continue until r successes have been obtained.

The random variable of interest,is the number of failures that precede theth success. may take any value greater than or equal to 0. Letdenote the probability mass function ofThe eventis equivalent toS's in the firsttrials and an S on the ()th trial. Ifandthen there must be four S's in the first 14 trials and the fifteenth trial must be an S. Since the trials are independent,

The first factor here is only the binomial probability of gettingS's intrials:

Multiplying this bygives

Like the normal binomial expansion, the negative binomial distribution is well defined even when r is not an integer. In this case we have the generalized negative binomial distribution.

The mean and variance are given by

and

Example: A paediatrician wishes to recruit five couples, each expecting their first child. Let be the probability that the couple agree to be recruited. What is the probability that fifteen couples are asked before the required five agree?

We have and