Theorem
If
is a Cauchy sequence in Euclidean
- space
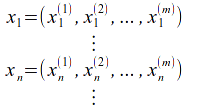
then each of the sequences
is a Cauchy sequence.
Proof
Let
Sinceis Cauchy, there exists
such that for
Hence,
and each of the sequencesis Cauchy.
Call Us 07766496223
Theorem
Ifis a Cauchy sequence in Euclidean- space
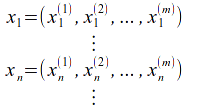
then each of the sequencesis a Cauchy sequence.
Proof
LetSinceis Cauchy, there existssuch that for
Hence,and each of the sequencesis Cauchy.