Proof That a Closed Subset of a Countably Compact Space is Countably Compact

Theorem

A closed subsetof a countably compact spaceis countably compact.

Proof

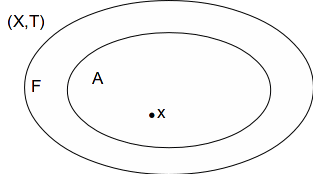
Letbe a countably compact set and letbe a closed subset of

Letbe an infinite subset ofA is also an infinite subset of a countably compact spaceAn accumulation pointofexists such that

Sinceis also an accumulation point ofSinceis closed, it contains all it's accumulation points, soHence an infinite subsetof a closed subsethas an accumulation pointhenceis countably compact.