Theorem
A completely regular space is regular.
Proof
A topological space
is completely regular if, for any closed subset
of
and any
a continuous function
exists such that for every
and
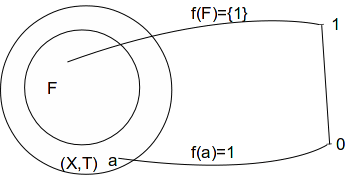
By hypothesis a continuous functionexists such that
andThe interval
is Hausdorff. Hence open disjoint subsets
and
ofexists such that
and since
is continuous
and
are open and
and
Henceis regular.