Theorem
A space![]() is said to be disconnected if the set
is said to be disconnected if the set![]() can be expressed as the union of at least two mutually exclusive, nonempty subsets of
can be expressed as the union of at least two mutually exclusive, nonempty subsets of![]()
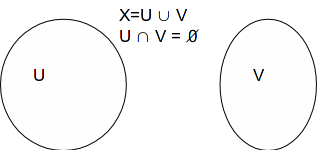
The set![]() is connected if it is not disconnected.
is connected if it is not disconnected.
Given a space![]() with the discrete topology, take
with the discrete topology, take![]() and consider the sets
and consider the sets![]()
Both these sets are open and![]() and
and![]()
and (X,T) is disconnected.
Any set with the trivial topology is connected since the only nonempty open subset of![]() is
is![]() itself.
itself.
