Proof That an Open Subspace of a Locally Compact Space is Locally Compact

Theorem

An open subspace of a locally compact space is locally compact.

Proof

Letbe an open subspace of a locally compact spaceand let

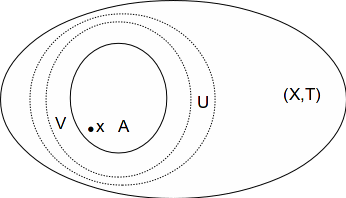
Letbe any neighbourhood ofsuch thatSinceis locally compact, a compact setexists such thathenceis locally compact.