Theorem
Let
with the indiscrete topology is not a T0 space.
Proof
A space
is a T0 space if for any two distinct elements
there is an open neighbourhood of one which does not contain the other.
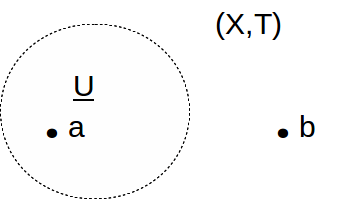
With the indiscrete topology
we cannot separate 0 from 1 or 1 from 0 henceis not a T0 space.
Consider the set
with the topology
For the distinct points 0 and 1, an open set
exists such that
but 
henceis a T0 space.
Each metric space is a T0 space since for distinct points
and
there exists
such that
hence
but