Proof That The First Countable Property is a Topological Property

Theorem

The first countable property is a topological property.

Proof

Supposeandare homeomorphic so that

Letbe a homeomorphism and letbe first countable. Letand let be an open subset ofcontaining

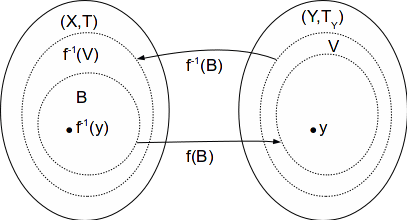
Sinceis a homeomorphismis a point inandis an open set insuch that

is first countable hencehas a countable local baseAn open setexists such thatthenwhereis open in