Theorem
|The intersection of a closed set
with a compact set
is compact.
Proof
Let
be an open cover of
so that
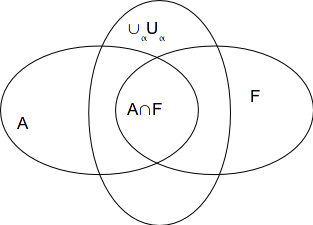
Then
and sinceis closed
is an open cover of
is compact so a finite subcover
of A exists.
Hence
and
is compact.
Call Us 07766496223
Theorem
|The intersection of a closed setwith a compact setis compact.
Proof
Letbe an open cover ofso that
Thenand sinceis closed is an open cover of
is compact so a finite subcoverof A exists.
Henceandis compact.