Theorem
The property of being homotopic is an equivalence relation.
Proof
1. f sim f . Let h:X times [0,1] rightarrw Y be defined by h(x,t)=f(x) then h(x,0)=h(x,1)=f(x) so f sim f.
2. f sim g. Since
there is a homotopy
with
Define
by
Then
and
Since
is continuous, so is
and
3.
then
Since
there is
such that
Sincethere is
such that
Define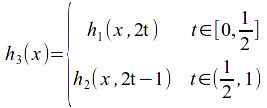
Then
and
so