Proof That the Reciprocal Sequence is Cauchy

Theorem

The sequencein the space of real numbers with the Euclidean topology, is a Cauchy sequence.

Proof

A Cauchy sequenceinis a Cauchy sequence if and only if, for all there existssuch that

TakeLetbe such that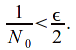

For anyhence

Henceis a Cauchy sequence.