A subdivision of a surface is called regular when every face has a boundary consisting of the same number of edges and the same number of edges meets at every vertex.
Euler's formula states
(1) where
is the number of vertices
is the number of edges
is the number of faces
If each face has
edges, the total number of lines is
If
edges enter each vertex, we can also write
Substitute these into (1) to obtain
This equation has simple solutions in the table below.
|
v |
f |
E |
V |
F |
|
v=E |
2 |
E |
2 |
F=E |
|
2 |
f=E |
E |
V=E |
2 |
>
These solutions are shown below.
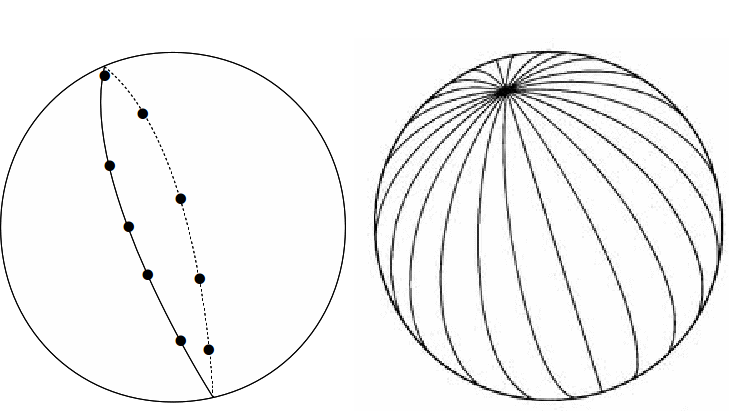
Other solutions exist. If
we obtain the trivial solutions
or
If
the only solution is
Suppose E>2 then
The only possible values ofandare 3, 4, 5. We can draw up the following table.
|
v |
f |
E |
V |
F |
Name |
|
3 |
3 |
6 |
4 |
4 |
Tetrahedron |
|
3 |
4 |
12 |
6 |
8 |
Cube |
|
3 |
5 |
30 |
12 |
20 |
Dedecahedron |
|
4 |
3 |
12 |
8 |
6 |
Octahedron |
|
5 |
3 |
30 |
20 |
12 |
Icosahedron |
In fact, if f=3 each face is a triangle. Triangles can be subdivided into triangles to form more regular subdivisions.
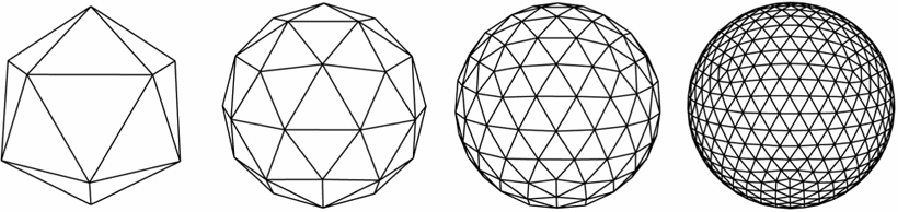
Similarly, ff f=4 each face is a rectangle. Rectangles can be subdivided into rectangles to form more regular subdivisions.