The Classification Theorem for Surfaces

The classification theorem of closed surfaces states that any connected closed surface is homeomorphic to some member of one of these three families:

1) the sphere;

2) the connected sum oftori,

3)the connected sum of k real projective planes, for

The surfaces 1) and 2) are orientable. The sphere can be regarded as the sum of no tori. The numberis called the genus of the surface.

The connected sum of two closed surfacesanddenotedis constructed by removing a disk from each of them and gluing the two boundaries together. The Euler characteristicofis the sum of the Euler characteristics of the surfaces, minus two:

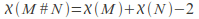
This is easily provable since the two boundaries can be joined with a cylinder. The number of edges increases by 5 (the two boundary edges plus one edge need to glue a rectangle into a cylinder and two edges from existing vertices, plus two more vertices in the boundary curves between the ends of the edge which make the cylinder) and the number of faces increases by one so the Euler characteristic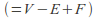changes by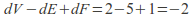over the sum of the Euler characteristics of the two surfaces. This is illustrated below.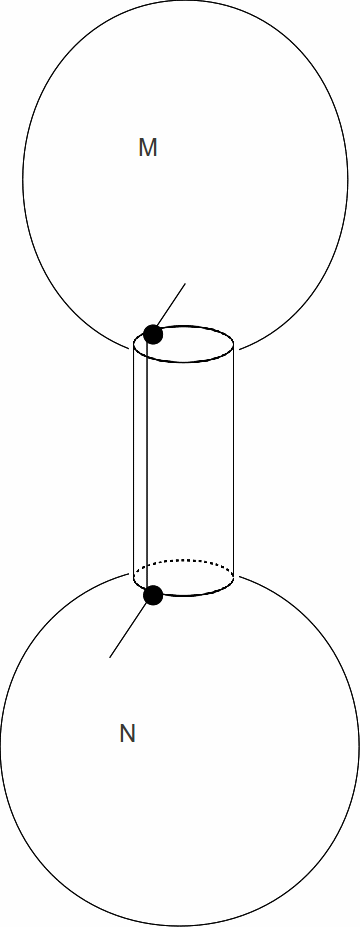

The sphere S is an identity element for the connected sum, meaning that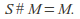This is because deleting a disk from the sphere leaves a disk, which simply replaces the disk deleted from M upon gluing.

Connected summation with the torus T is also described as attaching a "handle" to the other summand M. If M is orientable, then so is T # M. The connected sum is associative so the connected sum of a finite number of surfaces is well-defined.

The connected sum of two real projective planes is the Klein bottle. The connected sum of the real projective plane and the Klein bottle is homeomorphic to the connected sum of the real projective plane with the torus. Thus, the connected sum of three real projective planes is homeomorphic to the connected sum of the real projective plane with the torus. Any connected sum involving a real projective plane is nonorientable.

Since the sphere and the torus have Euler characteristics 2 and 0 respectively, it follows that the Euler characteristic of g connected tori is

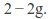
The surfaces in the third family are nonorientable. Since the Euler characteristic of the real projective plane is 1, the Euler characteristic of the connected sum of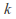of them is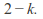

It follows that a closed surface is determined, up to homeomorphism, by two pieces of information: its Euler characteristic, and whether it is orientable or not. In other words, Euler characteristic and orientability completely classify closed surfaces up to homeomorphism. Any other surface is classified by the number of boundary curves, Euler characteristic and orientability.

Closed surfaces with multiple connected components are classified by the class of each of their connected components.