The Euler characteristic for a surface is given by F-E+V, or the number of faces - the number of edges+the number of vertices. The Euler characteristic is a topological invariant for a surface, so that surfaces with different Euler characteristics cannot be homeomorphic.
Any closed surface with no holes has Euler characteristic 2:
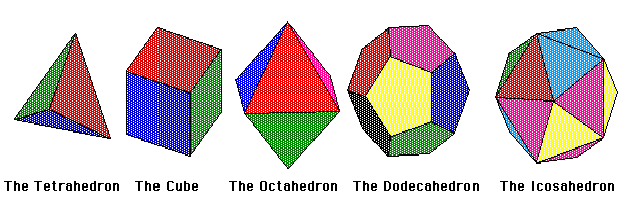
The five Platonic solids are shown above. Each has Euler characteristic 2.
|
Shape |
Number of Vertices, V |
Number of Edges, E |
Number of Faces, F |
Euler Characteristic F-E+V |
|
Tetrahedron |
4 |
6 |
4 |
2 |
|
Cube |
8 |
12 |
6 |
2 |
|
Octahedron |
6 |
12 |
8 |
2 |
|
Dodecahedron |
10 |
30 |
12 |
2 |
|
Icosahedron |
12 |
30 |
20 |
2 |
Finding the Euler Characteristic of more complicated shapes is well, more complicated. In general a shape must be cut up and the number of vertices, edges and faces found. It can be a complicated process.
