An affine transformation between two vector spaces consists of a linear transformation followed by a translation:
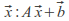
- where
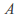is a matrix and
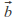is a vector. - In two dimensions this becomes
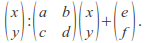
Affine transformations send lines to lines and preserve ratios of distances.
In general, an affine transformation is composed of linear transformations (rotation, scaling or shear)and a translation. Several linear transformations can be combined into a single one, so that the general formula given above is still applicable. This implies that the set of all affine transformations with A invertible forms a group.
Proof (for affine transformations in 2 dimensions):
Closure:
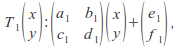
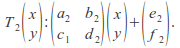
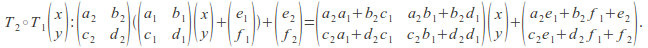
Identity: The identity is
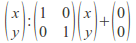and this is affine.Inverses:If
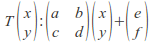then \[T^{-1}\]is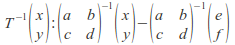
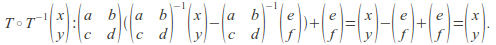
Similarly for
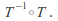
Other properties follow from the properties of matrix multiplication and addition of vectors.