If
\[\phi (x,y,z), \: \psi (x,y,z) \]
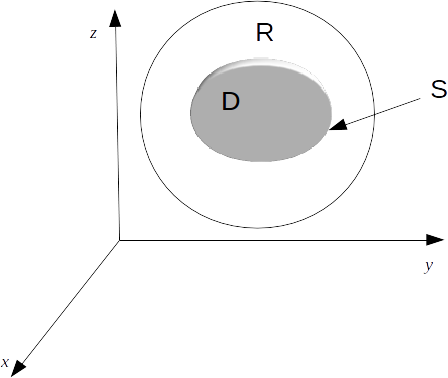
be harmonic functions with continuous first and second partial derivatives on a region \[R\]
containing a region \[D\]
with surface \[S\]
. If \[\phi (x,y,z), \: \psi (x,y,z) \]
satisfy the equations \[\nabla^2 \phi = f \phi , \: \nabla^2 \psi = f \psi ,\]
where \[f=f(x,y,z)\]
in \[D\]
\[\int \int_S \phi (\frac{\partial \psi}{\partial n} - \frac{\partial \psi}{\partial n} ) dS =0 \]
Proof
Green's Second Idenity can be written
\[\int \int_S ( \phi \frac{\partial \psi}{\partial n} - \psi \frac{\partial \phi}{\partial n} ) dS = \int \int \int_D (\phi \nabla^2 \psi - \psi \nabla^2 \phi )dV \]
Then
\[\int \int_S ( \phi \frac{\partial \psi}{\partial n} - \psi \frac{\partial \phi}{\partial n} ) dS = \int \int \int_D (\phi \nabla^2 \psi - \psi \nabla^2 \phi )dV = \int \int \int_D (\phi f \psi - \psi f \phi ) dV =0 \]
