\[xy\]
plane is given by \[I_P \int_S r^2 \rho (x,y) dS\]
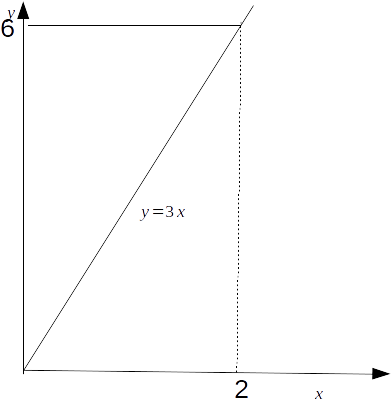
\[\rho=1\]
\[\begin{equation} \begin{aligned} I &= \int^2_0 \int^6_{3x} (x^2 +y^2) dy dx \\ &= \int^2_0 [x^2 y +y^3/3]^6_{3x} dx \\ &= \int^2_0 ((6x^2 + 72) - (3x^3 + 9x^3)) dx \\ &= [2x^3 +72x-3x^4]^2_0 \\ &= (16+144 - 48)-0 = 112 \end{aligned} \end{equation}\]
