\[xy\]
plane. A particle on the surface of the ellipse is made to move on the surface of the ellipse as the ellipse rotates. What will be the velocity and acceleration of the particle?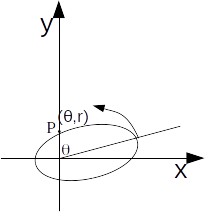
\[b, \; a\]
respectively, the coordinates of a point on the surface of the ellipse with origin at one focus is \[(r, \theta )\]
in polar coordinates with \[r= \frac{b^2}{a(1- ecos \theta )}\]
and the velocity is \[\frac{dr}{dt}= - \frac{eb^2 \dot{\theta} sin \theta }{a(1-e cos \theta )^2} \]
.The acceleration is
\[\frac{d^2r}{dt^2}= - \frac{eb^2 (\ddot{\theta} sin \theta + \dot{\theta}^2 cos \theta )}{a(1-e cos \theta )^2} - \frac{2e^2b^2 (\dot{\theta}^2 sin^2 \theta}{a(1-e cos \theta )^3} \]
.