\[\theta_1 , \: \theta_2 , \: \theta_3 , \:\]
withe the vertical.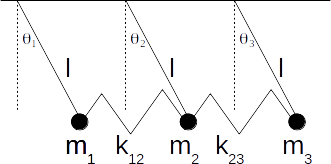
\[\mathbf{F} = m \mathbf{a}\]
to each mass horizontally and use \[a= l \ddot{\theta}\]
For \[m_1\]
: \[m_1 l \ddot{\theta}_1=- m_1g sin \theta_1+k_{12} (l \ sin \theta_2- l sin \theta_1)\]
For
\[m_2\]
: \[m_2 l \ddot{\theta}_2=- m_2g sin \theta_2-k_{12} (l \theta_2- l \theta_1)+k_{23} (l \theta_3- l \theta_2)=m_2g sin \theta_2+k_{12}l sin \theta_1-(k_{12}+k_{23})l sin \theta_2 + k_{23}l sin \theta_3\]
For
\[m_3\]
: \[m_3 l \ddot{\theta}_3=-m_3g sin \theta_3-k_{23} (l \theta_3- l \theta_2)\]
We can cancel throught by
\[l\]
and if we assume the oscillations are very small then we can use the approximation \[sin \theta \simeq \theta\]
.
The equations become\[m_1 \ddot{\theta}_1=- m_1g \theta_1+k_{12} ( \theta_2- \theta_1)\]
\[m_2 \ddot{\theta}_2=-m_2g \theta_2+k_{12} \theta_1-(k_{12}+k_{23}) \theta_2 + k_{23} \theta_3{/jtex}
{jatex options:inline}m_3 \ddot{\theta}_3=-m_3g \theta_3-k_{23} ( \theta_3- \theta_2)\]
{jatex options:inline}m_3 \ddot{\theta}_3=-m_3g \theta_3-k_{23} ( \theta_3- \theta_2)\]
Collect the
\[\theta\]
's and divide by \[m_1 , \: m_2, \: m_3\]
respectively.\[ \ddot{\theta}_1=- \frac{ m_1g+k_{12}}{m_1} \theta_1+\frac{k_{12}}{m_1} \theta_2\]
\[ \ddot{\theta}_2=\frac{k_{12}}{m_2} \theta_1- \frac{m_2g+k_{12}+k_{23}}{m_2} \theta_2 + \frac{k_{23}}{m_2} \theta_3\]
\[ \ddot{\theta}_3=\frac{k_{23}}{m_3} \theta_2 -\frac{m_3g+k_{23}}{m_3} \theta_3\]
In matrix form this becomes
\[\begin{pmatrix} \ddot{\theta}_1 \\ \ddot{\theta}_2 \\ \ddot{\theta}_3 \end{pmatrix} = \left( \begin{array}{ccc} - \frac{m_1g+k_{12}}{m_1} & \frac{k_{12}}{m_1} & 0 \\ \frac{k_{12}}{m_2} & - \frac{m_2g+k_{12}+k_{23}}{m_2} & \frac{k_{23}}{m_2} \\ 0 & \frac{k_{23}}{m_3} & \frac{m_3+gk_{23}}{m_3} \end{array} \right)\]
The natural frequencies are the square roots of the negatives eigenvalues of this matrix,
\[\omega= \sqrt{- \lambda}\]
. 