\[L\]
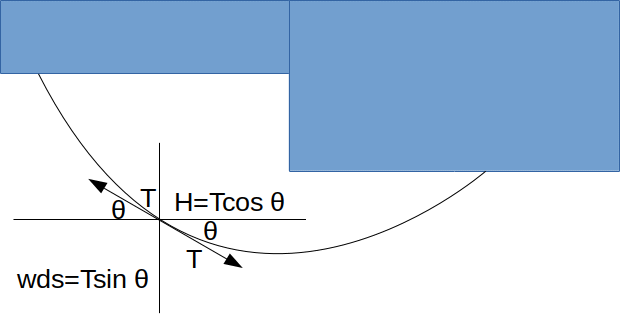
of chain is hung from an uneven ceiling. The ends of the chain are fixed to two points some distance apart. What will be the shape of the chain?Let the chain lie in the vertical
\[xy\]
plane. An small length \[ds\]
of chain of wight per unit length \[w\]
is subject to a vertical for \[T sin \theta =wds\]
; and a horizontal force \[T cos \theta =H\]
.We must have
\[\frac{Tsin \theta}{Tcos \theta}= \frac{wds}{H}= \frac{W}{H} ds= \frac{W}{H} \sqrt{(dx)^2+(dy)^2}\]
. Then \[\frac{Pd^2y}{dx^2} = \frac{w}{H} \sqrt{1+ (\frac{dy}{dx})^2}\]
.Let
\[\frac{dy}{dx}=p\]
then we can write the equation as \[\frac{dp}{dx}= \frac{w}{H} \sqrt{1+p^2} \rightarrow \int \frac{1}{\sqrt{1+p^2}}dp = \frac{w}{H} \int dx\]
.
\[sinh^{-1} p = \frac{w}{H}x+c\]
.We can set the
\[y\]
axis to go through the minimum of the curve, where \[\frac{dy}{dx}=c=p=0\]
then \[\frac{dy}{dx}=sinh (\frac{w}{H} x)\]
. Integration now gives \[y=\frac{H}{w} cosh ( \frac{w}{H} x )+k\]
.Choosing the
\[x\]
at a distance \[\frac{H}{w}\]
below the lowest point of the chain, the \[k=0\]
and the equation of the chain is \[y= \frac{H}{w} cosh ( \frac{w}{H} x)\]
. 