The Hamiltonian
represents the energy of the system which is the sum of kinetic and potential energy, labelled
and
respectively. For a one dimensional system, we may write
so
where
Note that
is a function of
only and
is a function of
only. In generalis a function of
only andis a function of the coordinates, however they are defined.
The value of the Hamiltonian is the total energy of the system. For a closed system, it is the sum of the kinetic and potential energy in the system and is conserved. The Hamiltonian equations give the time evolution of the system. These are
where
and
The time-derivative of the momentumequals the force acting so the first Hamilton equation means that the force on the particle equals the rate at which it loses potential energy with respect to changes in
its position.
The time-derivative of
here means the velocity: the second Hamilton equation here means that the particle’s velocity equals the derivative of its kinetic energy with respect to its momentum.
We can derive Hamilton's equations by looking at how the total differential of the Lagrangian depends on time, generalized positions
and generalized velocities
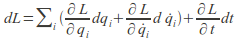(1) - Now use
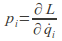and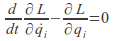
to give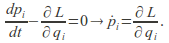
Substitute these into (1):
which we can rewrite as
and rearrange to get
The term on the left-hand side is the Hamiltonian so
where the second equality holds because it is equal to
Associating terms from both sides of the equation above yields Hamilton's equations
and