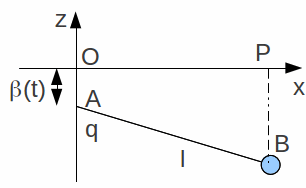
Deriving the Hamiltonian and Lagrangian for a time dependent system is not much more complicated than for the time independent case. The pendulum of mass
and length
below is made to oscillate at A with the distance OA given by
The potential energy is given by
The kinetic energy is given by
Hence
The Lagrangian is
Where
may be ignored since it is a function of
only and ignoring it returns the same Lagrangian equation of motion.
We can now find the Hamiltonian by expressing the Lagrangian in terms of
and
to obtain
Then