Velocity - Time Graphs, Area and Distance
There are two very important things to remember about velocity – time graphs.
The distance travelled is the area under the graph.
The gradient or slope of the graph is equal to the acceleration. If the gradient is negative, then there is a deceleration. We may use the equations
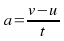(1) or some rearrangement of this equation.
Example. A car starts on a journey. It accelerates for 10 seconds at
It then travels at a constant speed for 50 seconds before coming to rest in a further 4 seconds.
a)Sketch a velocity – time graph.
b)Find the total distance travelled.
c)Find the deceleration when the car is coming to a stop at the end.
d)Find the average speed.
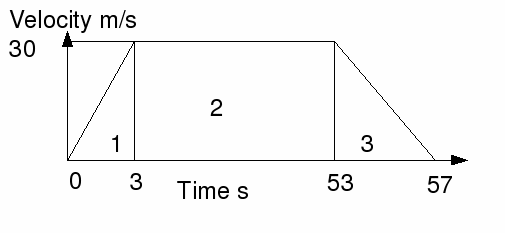
Hence we may draw a straight line from (0,0) to (3,30). During the second part the car is travelling at a constant speed of 30m/3. Hence we can draw a straight line to (3,30)+(50,0)=(53,30). During the last part, which takes a further 4 seconds the car comes to a rest, and it's final velocity will be zero. Hence we can draw a straight line to (57,0). We can now draw the velocity time graph.b)Distance travelled = Area under the graph. The graph is a trapezium so use the formula for the area of a trapezium:
c)During the final part of the journey the velocity decreases from 30 to 0 in 4 seconds so
d)
