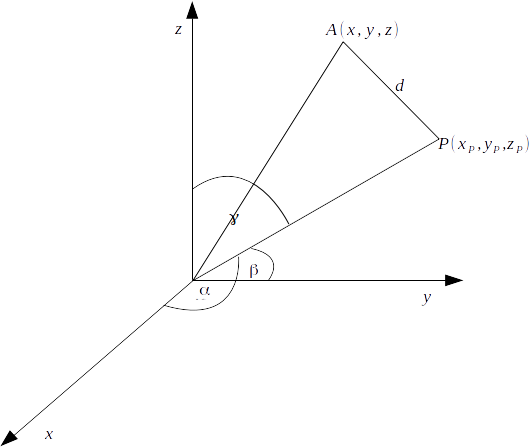
The direction cosines of a line drawn from the origin
\[O\]
to the point \[P(z_P , y_P , z_P)\]
are given by \[(\alpha , \beta , \gamma ) = (\frac{x_P}{\sqrt{x^2_P + y^2_P + z^2_P}} , \frac{y_P}{\sqrt{x^2_P + y^2_P + z^2_P}} , \frac{z_P}{\sqrt{x^2_P + y^2_P + z^2_P}}\]
\[\alpha^2 + \beta^2 + \gamma^2 =1\]
(1) and \[\frac{\alpha^2 y^2_P + \alpha^2 z^2_P}{1- \alpha^2} = \frac{x^2_P / OP^2 (OP^2 -x^2_P)}{1-x^2_P / OP^2} =\frac{x^2_P (OP^2 - x^2)}{OP^2 - x^2_P} =x^2_P \]
so \[x^2_P = \frac{\alpha^2 y^2_P + \alpha^2 z^2_P}{1- \alpha^2} \]
Hence
\[y_P^2 = \beta^2 (x^2_P + y^2_P +z^2_P ) =\beta^2 (\frac{\alpha^2 y^2_P + \alpha^2 z^2_P}{1- \alpha^2} + y^2_P +z^2_P ) \]
which simplifies to \[\beta^2 (y^2_P + z^2_P ) = y^2_P (1- \alpha^2 ) \]
From the equations for the direction cosines we obtain:
\[\beta^2 z^2_P = \gamma^2 y^2_P\]
(1)\[\beta^2 x^2_P = \alpha^2 y^2_p\]
(2)\[\gamma^2 z^2_P = \alpha^2 2 Z^2_P\]
(3)\[\beta^2 z^2_P = \gamma^2 y^2_P\]
The distance from
\[(x,y,z)\]
and \[(x_P ,y_P ,z_P)\]
is \[d= \sqrt{(x-x_P)^2 +(y-y_P)^2 + (z-z_P)^2}\]
From the diagram,
\[OA^2 = d^2 +OB^2\]
so \[x^2+y^2+z^2 =(x-x_P)^2 +(y-y_P)^2 + (z-z_P)^2 + x^2_P+y^2_P+z^2_P\]
which simplifies to \[x^2_P + y^2_P + z^2_P = xx_P + yy_P + zz_P\]
Substitute (1) and (2) into this equation to obtain
\[x_P+\frac{\beta^2}{\alpha^2} x_P + \frac{\gamma^2}{\alpha^2} x_P = x+y \frac{\beta}{\alpha}+ z \frac{\gamma}{\alpha}\]
which simplifies to
\[x_P= \alpha^2 x + \alpha \beta y + \alpha \gamma z\]
(4)From the equaton for
\[d\]
above \[d= x^2 +y^2 +z^2 +x^2_P +y^2_P +z^2_P -2xx_P -2yy_P -2zz_P \]
Substitute (1), (2), (3) and (4) into this to obtain
\[\begin{equation} \begin{aligned} d^2 &= x^2+y^2+z^2 +\frac{1}{\alpha^2} (\alpha^2 x + \alpha \beta y + \gamma \alpha z)^2 \\ &- 2 (\alpha^2 x+ \alpha \beta y + \alpha \gamma z)(x+y \frac{\beta}{\alpha} +z \frac{\gamma}{\alpha}) \\ &= x^2 +y^2 +z^2 +(\alpha^2 x +\alpha \beta y + \alpha \gamma z)(-x -\frac{\beta}{\alpha} - \frac{\gamma}{\alpha}z ) \\ &=x^2 (\beta^2 + \gamma^2)+ \gamma^2 (\alpha^2 + \gamma^2) \\ &+ z^2 (\alpha^2 + \beta^2) - 2 \alpha \beta xy -2 \alpha \gamma xz -2 \beta \gamma yz \\ &= \alpha^2 (y^2 + z^2)+ \beta^2 (x^2 + z^2) \\ &+ \gamma^2 (x^2 + y^2) - 2 \alpha \beta xy -2 \alpha \gamma xz -2 \beta \gamma yz \end{aligned} \end{equation} \]
\[I_P = \int \int \int d^2 \rho (x,y,z) dxdydz\]
where
\[\rho (x,y,z)\]
is the density at \[(x,y,z)\]
.Substituting the equation derived for
\[d^2\]
above gives\[\begin{equation} \begin{aligned} I_p &= \alpha^2 \int \int \int \rho (y^2 + z^2)dx dy dz + \beta^2 \int \int \int(x^2 + z^2)dx dy dz \\ &+ \gamma^2 \int \int \int (x^2 + y^2)dx dy dz - 2 \alpha \beta \int \int \int xy dx dy dz -2 \alpha \gamma \int \int \int xz dx dy dz -2 \beta \gamma \int \int \int yz dx dy dz \\ &= \alpha^2 I_x +\beta^2 I_y + \gamma^2 I_z - 2 \alpha \beta I_{xy} - 2 \alpha \gamma I_{xz} - 2 \beta \gamma I_{yz}\end{aligned} \end{equation} \]
This is the equiation of the ellipsoid of inerta.
