The Cauchy - Riemann Equations

The Cauchy – Riemann equations lay down the conditions for a complex valued function to be differentiable at a point, but they also have applications in fluid dynamics. If thenis differentiable at a point if:

Let the functionsandbe the horizontal and vertical components of the velocity field of a steady incompressible, irrotational flow in two dimensions. The equations are occur in fluid mechanics from consideration of the velocity potentialandare found from the velocity potential

The condition that the flow be incompressible is that

and the condition that the flow be irrotational is that

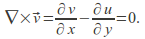
If we define the differential of a functionby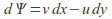then the incompressibility condition is the integrability condition for this differential: the resulting function is actually the stream function because it is constant along flow lines. The first derivatives ofare given by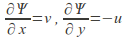and the irrotationality condition implies thatsatisfies the Laplace equation: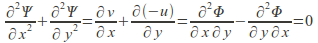 The harmonic function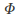(harmonic since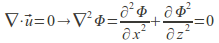) that is conjugate tois the velocity potential.

Every analytic function corresponds to a steady incompressible, irrotational fluid flow in the plane. The real part is the velocity potential, and the imaginary part is the stream function.