The Navier - Stokes Equation

The Navier – Stokes equation models the behaviour of a fluid element because of the forces acting on it, including viscous forces. When the viscous forces are ignored, the equations become Euler's equation. The equation is difficult to solve, and analytic solutions are only found for very simple examples. Usually the terms of the equation are assessed for important so that some can be dropped and the equation simplified.

The Navier – Stokes equation is

or

Proof: The fluid velocityof an inviscid (ideal) fluid of densityunder the action of a body forceis determined by the equation:

(Euler’s equation) whereis the pressure. This equation is supplemented by an equation describing the conservation of mass. For an incompressible fluid this is simply

Real fluids are never truly inviscid. To take account of viscous forces we introduce the stress tensorthe- component of stress on a surface elementthat has a normalpointing in the- direction then ifis the stress on a small surface element δS with unit normal(1)

Proof of (1) : Taketo be the large face of the tetrahedron shown in the figure below.

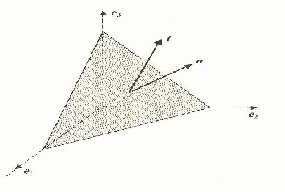
Apply Newton’s 2nd law to the fluid in the tetrahedron. For definiteness consider the-component of the force. The force of the surrounding fluid on the large face isThe- component of the force on the ‘back’ face is(since the normal is in thedirection). Similarly for the two faces with normalsandThus the- component of the

total force exerted by surrounding fluid on the tetrahedron is (2) (indicates summation over). This force (plus any body force) will be equal, from Newton’s 2nd law, to the mass of the element () multiplied by its acceleration. Ifis the linear

length scale of the tetrahedron thenandThus if we letthen the term (2) clearly dominates and hence

The ith component of force exerted by the surrounding fluid on a fluid blob with surfaceand volumeis given by

usingtogether with the divergence theorem. Applying Newton’s 2nd law to an arbitrary fluid blob then leads to the equation of motion:

Applying an argument involving angular momentum to a tetrahedron, similar to the argument above using linear momentum, leads to the result that the tensoris symmetric.

In order actually to solve it is necessary to relate the stress tensorto the fluid velocityFor simplicity we consider only incompressible fluids for which the stress tensor is assumed to take the form- a Newtonian fluid, e.g. water and most gases under modest conditions - whereis the viscosity.

Sincethe mean of the three normal stresses.

The final step in deriving the Navier - Stokes equation is to substituteforinto equationThis leads to the equation (assuming constant viscosity),- The Navier - Stokes equation.