Velocity potential is used in fluid dynamics, when a fluid occupies a simply-connected region – no sources or sinks - and is irrotational, so the velocity field
has zero curl:
As a result,can be represented as the gradient of a scalar function:
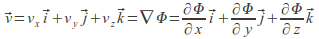in Cartesian coordinates. Given the velocity field we can find the velocity potential by integration.
The velocity potential is not unique. If
is a constant then
is also a velocity potential for
Conversely, if
is a velocity potential forthen
for some constant
In other words, velocity potentials are unique up to a constant.
Example : Suppose
shown below:
Example:
Find the velocity potential.
These are all equal. Put the first and second equal. Then
are both functions of
only and both are equal to
which is a function of
and
so
and
where is an arbitrary constant.