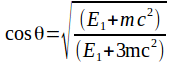The Elastic Collision of Two Particles

Consider the collision of two particles, one of massmoving with speed u which collides head on with a particle ofat rest in its own inertial frame O', relative to which particle 1 has speed along the positive x axis. Having particle 2 at rest in its own inertial frame makes the solution simpler, and the speed of each particle in any other inertial frame can be found using the velocity transformations.

Before Collision

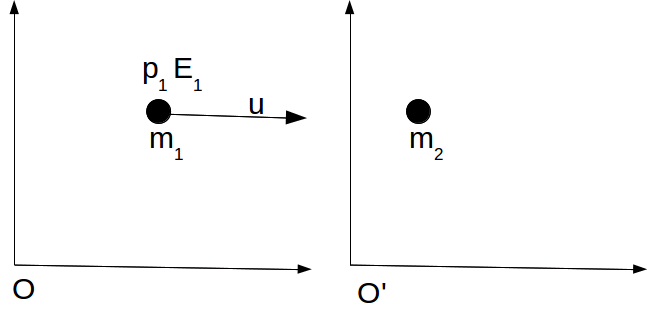
After Collision

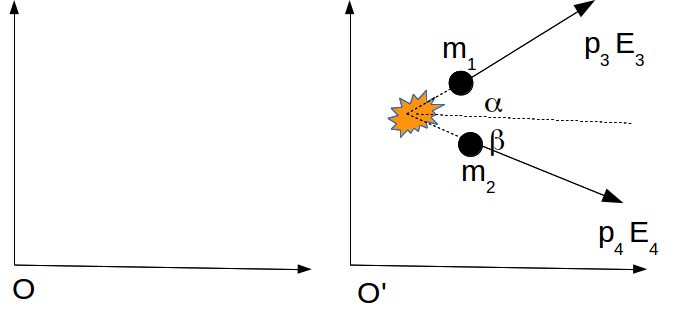
Conservation of momentum gives

(3)

(4)

Conservation of energy gives(5)

Since(6) we have

Ifandthen from (4),then from (5) that(7)

Putandin (3) to obtain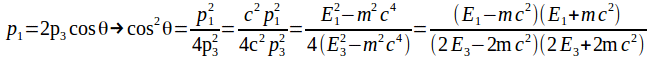

From (7) then we obtain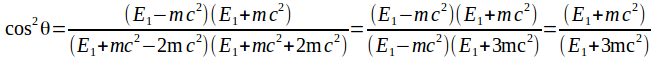

Hence