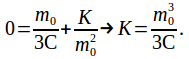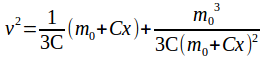As raindrops fall, they tend to grow. If a raindrop of mass![]() is falling through a stationary cloud, then for each infinitesimally small amount that the raindrop grows by, momentum is conserved at the instant of growth. At the same time, gravity is pulling the raindrop down with a force
is falling through a stationary cloud, then for each infinitesimally small amount that the raindrop grows by, momentum is conserved at the instant of growth. At the same time, gravity is pulling the raindrop down with a force![]() Suppose the raindrop is accumulating mass at a constant rate C kg/s. If during a time
Suppose the raindrop is accumulating mass at a constant rate C kg/s. If during a time![]() the momentum of the raindrop increases by
the momentum of the raindrop increases by
![]() then assuming
then assuming![]() is constant during the time interval
is constant during the time interval![]()
![]()
Diving by![]() gives
gives
![]()
Now let![]() to give the differential equation
to give the differential equation![]()
If the mass of the raindrop is increasing at the constant rate C with respect to x then![]()
![]() and
and![]() so
so![]()
Write![]()
The equation becomes![]()
Now divide by![]() and write
and write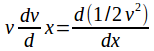 :
: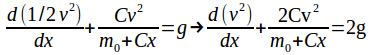
We can solve this equation using the integrating factor method: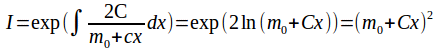
The equation now becomes![]()
Hence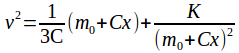
If![]() when
when![]() then
then