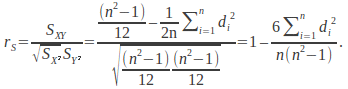Spearman's Rank Correlation Coeffcient
The correlation coefficientmeasurements the goodness of fit of a set of points
toa straight line but two quantities may in fact observe a perfectcorrelation without all the points lying on a straight line. Thequantities x and y have a perfect though non linear relationship asshown on the graph below. The relationship is perfect for the rangesof x and y in that if x increases then so does y.
The correlation betweenvariables
and
thathave a non linear relationship may be better expressed by a functionof the variables called the rank correlation coefficient. The rankcorrelation coefficient is found by ordering the
interms of size, labelling them
Each
hasa corresponding
butwhen the
areput into order the
maynot have the same order as the
Supposethehaveranks
Labelthe ranks of theas
(thoughwe may in fact take them as
).
For each
find
andfind
insome order and each of these is equal to
so
insome order and each of these is equal to
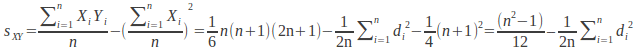
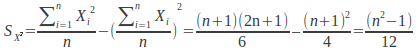and similarly for
Spearman's Rank correlationcoefficient is given by
