For the diagram below, if
\[\]
is the angle in the triangle ABC subtended by the radius of the circle from the midpoint of a side of the base, then \[tan \alpha = \frac{r}{x/2} = \frac{2r}{x}\]
.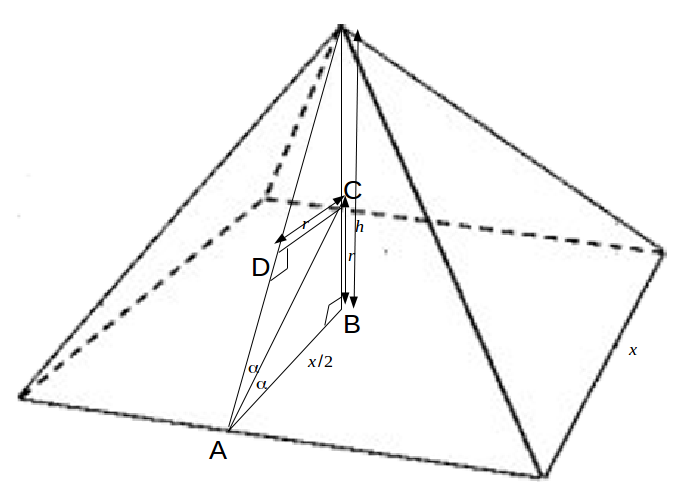
\[\alpha\]
and angle DAB is \[2 \alpha\]
.From the diagram,
\[tan 2 \alpha = \frac{h}{2/x} = \frac{2h}{x}\]
.Now use the identity
\[tan 2 \alpha = \frac{2 tan \alpha}{1- tan^2 \alpha}\]
to obtain\[\frac{2h}{x} = \frac{4r/x}{1-(2r/x)^2} = \frac{4rx}{x^2 - 4r^2}\]
We can rearrange this as a quadratic in
\[r\]
, obtaining\[8hr^2+4rx^2-2hx^2=0\]
.Solving this gives
\[r=\frac{-4x^2 \pm \sqrt{16x^4 +64h^2x^2}}{16h} = \frac{-x^2 \pm x \sqrt{x^2+4h^2}}{4h}\]
Only the
\[+\]
option gives a valid value of \[r\]
so \[r= \frac{-x^2 + x \sqrt{x^2+4h^2}}{4h}\]
